福島宙輝(神戸大学)
八木俊匡(株式会社アルタレーナ)
大田 快斗(fomalhaut coffee)
味と形のマルチモーダルな表象
C. Velasco, A. Woods, J. Liu, and C. Spence, “Assessing the Role of Taste Intensity and Hedonics in Taste – Shape Correspondences,” vol. 29, pp. 209–221, 2016.
A. J. Bremner, S. Caparos, J. Davidoff, J. de Fockert, K. J. Linnell, and C. Spence, “‘Bouba’ and ‘Kiki’ in Namibia? A remote culture make similar shape–sound matches, but different shape–taste matches to Westerners,” Cognition , vol. 126, no. 2, pp. 165–172, Feb. 2013.
C. Velasco, A. T. Woods, O. Petit, A. D. Cheok, and C. Spence, “Crossmodal correspondences between taste and shape , and their implications for product packaging : A review q,” Food Qual. Prefer., vol. 52, no. 4, pp. 17–26, 2016.
C. Spence et al., “On tasty colours and colourful tastes? Assessing, explaining, and utilizing crossmodal correspondences between colours and basic tastes,” 2012.
現時点での体系的なレビュー論文
Spence, C. (2023). Explaining visual shape–taste crossmodal correspondences. Multisensory Research, 36(4), 313-345.
多くの実験から、丸い形は甘さ・クリーミーさ、角ばった形は酸味・苦味・辛さ・炭酸感と一貫して対応づけられることが示されている。
この対応は、食べ物そのものの形だけでなく、皿・グラス・パッケージ・ロゴ・フォントなど、食の周辺デザインにも及び、味の「期待」や一部の「実際の味評価」を弱くバイアスしうる。
・味経験の「広がり/鋭さ」といった空間的な質感の直接記述、
・味の時間プロファイルとの時空アナロジー(甘味=ゆるやかなカーブ、酸味=鋭い立ち上がり)、
・甘さ=好ましい形、苦味=脅威的な形という情動・快不快の媒介、
・パッケージ・グラス・ロゴなどへの経験的な学習・連想
が重なっていると考えられる。
こうした知見は、マルチセンサリーな食体験デザインやマーケティング(VR環境、フォントや器の形状操作など)で活用されつつあるが、現実場面では「高級感・健康感・自然さ・量感」など他の意味づけも同時に働くため、形だけで味を強くコントロールするのは難しい、という点も強調される。
本研究の目的
味や香りといった風味の主観的表象をマルチモーダルに記述するための基盤として、
抽象図形を用いた多肢選択式の刺激セットを開発する
味の主観的表象(⾔語・⾮⾔語表象)と化学的成分、脳活動の三者はどのように相関しているか?
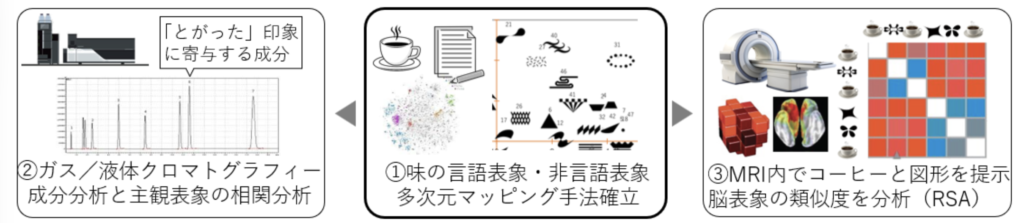
課題①:味の主観的経験を⾔語表象・描画表象実験で取得・分析する⽅法論を構築する
課題②:⾼次味質表現と描画表象を、ガス/液体クロマトグラフィー分析から説明する
課題③: fMRIでコーヒー刺激を提⽰し、脳表象空間と図形表象空間の相同性を解明する
人は味のセンサーデータのすべてを表象しているわけではない
言語はセンサーデータの写像ではない
ある部分は言語的に表象されやすく、ある部分は図形で表象されやすい
多様な表象相の特徴を捉えたい
データセット


特徴量を取ってくる
目標:750種は多すぎるので、24〜48クラスタくらいにしたい
図形の特徴量からクラスタリングして、代表図形を選出する
図形の特徴量どうやって取る?
面積、円形度、尖度、頂点数…
pythonでは 関数 regionprops でおおまかに取得可能
https://jp.mathworks.com/help/images/ref/regionprops.html
https://www.mitani-visual.jp/products/image_analys_ismeasurement/winroof2023
もともとの想定ユースケースは顕微鏡画像の細胞を数えるなど


Winroofを試してみた
① 位置・座標に関する特徴(図形が画像内でどこにあるか)
始点X, 始点Y
外接長方形 始点X, 始点Y, 終点X, 終点Y
中心X, 中心Y
重心 X, 重心 Y
絶対最大長 始点X, 始点Y, 終点X, 終点Y
最大高さ X, 最大高さ Y
最大深さ X, 最大深さ Y
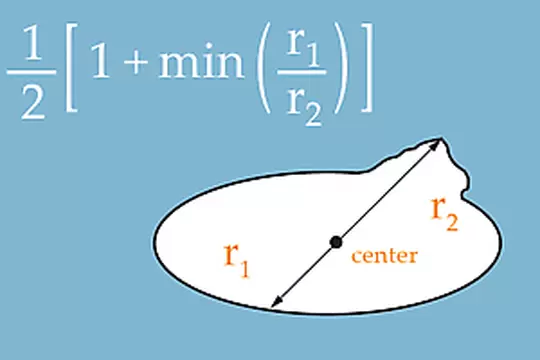
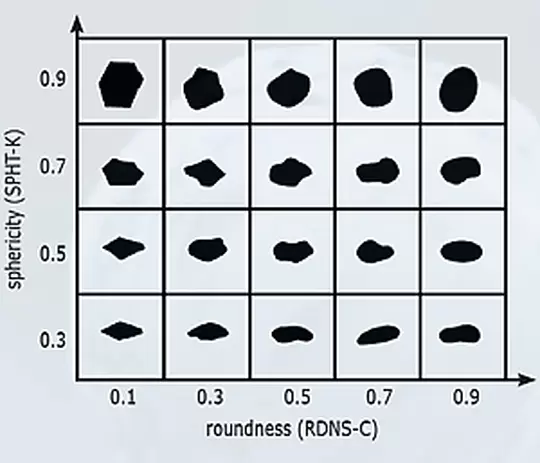
② 大きさ・面積・幅の特徴(大きさ・体積・等価円など)
面積, 面積Ⅰ, 面積Ⅱ
円相当径, 半径
球体体積
包絡面積
サイズ (pixel)
流体直径
穴面積, 穴面積率, 穴含む面積
物体幅 最大, 最小, 平均
対角幅
中央幅
最大内接円径, 最大内接円面積
体積, 表面積, 表面積Ⅱ
側面を除く表面積, 側面を除く表面積Ⅱ
包絡面積

③ フェレ長・径比など形状の比率(長さ・短さ・細長さ・丸さの指標)
フェレ 水平, 垂直
フェレ 長径Ⅱ, 短径Ⅱ, 径比Ⅱ, 面積率Ⅱ
フェレ 長径Ⅲ, 短径Ⅲ, 径比Ⅲ, 面積率Ⅲ
円形度, 円形度Ⅱ
針状比
径比率
凹凸度
線形度
細長さ・丸さ・偏りなど、形そのものの特徴を示す。
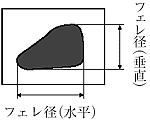
フェレ長(Feret diameter)は、「物体をある角度から見たときの投影の長さ」。
水平フェレ長・垂直フェレ長は物体の方向性を反映する。
「ごつごつ」か「滑らか」か(凹凸度)、「細長い」か「丸い」か、「縦長」か「横長」か
④ 長さ・距離に関する特徴(境界の長さ、中心距離、骨格など)
周囲長, 周囲長Ⅱ
骨格長さ
曲線長さ
中央線長さ
端点 / 本数
中心距離 最大, 最小, 平均, 標準偏差
重心距離 最大, 最小, 平均, 標準偏差
切断長 最大, 最小, 平均

⑤ モーメント(形の重み・ゆがみ・方向性)
モーメント X, Y
モーメント XX, YY, XY
モーメント GXX, GYY, GXY
モーメント GUU, GVV, GUV
方向 (°)
方位角 (°)
⑥ 楕円近似・弦長・断面形状(楕円フィットや断面形状による特徴)
楕円 長軸, 短軸, 長短比
水平弦長 最大, 最小, 平均
垂直弦長 最大, 最小, 平均
水平等分径
垂直等分径
⑦ 高さ・深さの特徴(3D形状)(最大高さ・重心高さなど高さ方向の特徴)
最大高さ, 最大深さ
重心高さ(最大, 最小, 平均, 標準偏差)
重心深さ(最大, 最小, 平均, 標準偏差)
⑧ 光学的・その他の特徴
最大輝度 (%)
輝度差
面積率 (%)
収縮率 (%)
個数
円ソーエッジ(凹最大値・凸最大値・平均・合計)
分析の結果サンプル
| No. | 画像ファイル名 | 始点X (pixel) | 始点Y (pixel) | 外接長方形 始点X (pixel) | 外接長方形 始点Y (pixel) | 外接長方形 終点X (pixel) | 外接長方形 終点Y (pixel) | 中心X (pixel) | 中心Y (pixel) | フェレ 水平 (pixel) |
| 1 | 101_e | 122.000000 | 178.000000 | 14.000000 | 178.000000 | 991.000000 | 827.000000 | 502.500000 | 502.500000 | 978.000000 |
| 2 | 101_a | 488.000000 | 85.000000 | 16.000000 | 85.000000 | 990.000000 | 916.000000 | 503.000000 | 500.500000 | 975.000000 |
| 3 | 101_b | 464.000000 | 260.000000 | 12.000000 | 260.000000 | 989.000000 | 745.000000 | 500.500000 | 502.500000 | 978.000000 |
| 4 | 101_c | 197.000000 | 292.000000 | 7.000000 | 292.000000 | 991.000000 | 711.000000 | 499.000000 | 501.500000 | 985.000000 |
| 5 | 101_d | 501.000000 | 57.000000 | 19.000000 | 57.000000 | 984.000000 | 892.000000 | 501.500000 | 474.500000 | 966.000000 |
128次元の特徴量によるクラスタリング(48クラスタ)

クレンジングの検討
「連続図形」の扱い (削除)
複合図形の扱い (削除)
hole図形の扱い(図と地、削除)
酷似する画像の削除
クレンジング後のクラスタリング結果
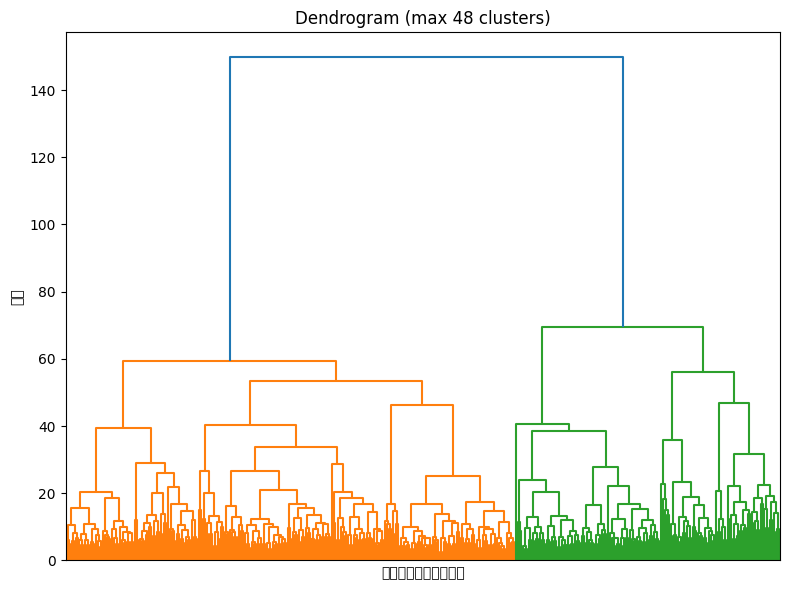

48クラスタの代表図形一覧

ランダム表示

今後の実験
プロテイスター10名による図形官能評価(1月)
→ ガスクロマトグラフィー・液体クロマトグラフィーによる成分分析(2月)
図形の特徴量と成分分析の相関分析
将来的には言語表象(オノマトペなど)との統合的な分析